1.线性表

利用两个线性表LA和LB分别表示两个集合A和B，现要求进行如下运算：B=A∩B。

注意:

1. 前置代码已经给出，请在该代码的基础上完成规定要求。

2. 测试用例2，表示没有任何输出，并不是输出回车符号。

3.输入时，先输入线性表的元素个数，然后输入各个元素。例如，输入：

   2

  1 2

   表示第一个线性表元素个数为2，元素分别为 1,2 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
#include <iostream>

using namespace std;
class List;
class LinkNode
{
    friend class List;

protected:
    LinkNode *link;
    int data;

public:
    LinkNode(LinkNode *p = NULL) { link = p; }
    LinkNode(int num, LinkNode *p = NULL)
    {
        data = num;
        link = p;
    }
    ~LinkNode(){};
};
class List
{
protected:
    int all;
    LinkNode *first;

public:
    List();

    void input();
    void output();
    int remove(int &a);
    void intersection(List *l2);
    int find(int a);
    void sort();
};
List::List()
{
    first = new LinkNode();
    all = 0;
}
void List::input()
{
    int num, val;
    cin >> num;
    while (num)
    {
        cin >> val;
        LinkNode *newnode = new LinkNode(val);
        newnode->link = first->link;
        first->link = newnode;
        num--;
    }
}
void List::output()
{
    LinkNode *node = first->link;
    while (node != NULL)
    {
        cout << node->data << endl;
        node = node->link;
    }
}
int List::remove(int &a)
{
    LinkNode *node = first;
    LinkNode *p;
    while (node->link != NULL)
    {
        if (node->link->data == a)
        {
            p = node->link;
            node->link = p->link;
            delete p;
            return 1;
        }
        node = node->link;
        return 0;
    }
}
int List::find(int a)
{
    LinkNode *node = first->link;
    while (node != NULL)
    {
        if (node->data == a)
        {
            return 1;
        }
        node = node->link;
    }
    return 0;
}
void List::intersection(List *l2)
{
    LinkNode *node = first;
    while (node->link != NULL)
    {
        if (!l2->find(node->link->data))
        {
            LinkNode *p = node->link;

            node->link = p->link;
            delete p;
        }
        else
        {
            node = node->link;
        }
    }
}
void List::sort()
{
    for (LinkNode *node1 = first->link; node1 != NULL; node1 = node1->link)
    {
        for (LinkNode *node2 = node1->link; node2 != NULL; node2 = node2->link)
        {
            int j;
            if (node1->data > node2->data)
            {
                j = node2->data;
                node2->data = node1->data;
                node1->data = j;
            }
        }
    }
}
int main()
{
    int k = 2;
    List l1, l2, l3;
    l1.input();
    // l1.output();
    l2.input();
    // l2.output();
    l1.intersection(&l2);
    l1.sort();
    l1.output();
    return 0;
}

2.链表

请按照建立的链表的顺序，输出第奇数个元素的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
/* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */

#include <iostream>

#include <stdio.h>

#include <stdlib.h>

using namespace std;

class List; //前视定义,否则友元无法定义

class LinkNode

{

    friend class List; //链表结点类的定义

private:
    LinkNode *link;

    int data;

public:
    LinkNode(LinkNode *ptr = NULL) { link = ptr; }

    LinkNode(const int &item, LinkNode *ptr = NULL)
    {
        data = item;
        link = ptr;
    }

    ~LinkNode(){};
};

class List

{ //单链表类的定义

private:
    LinkNode *first; //指向首结点的指针

public:
    List() { first = new LinkNode(); } // 带头结点

    ~List() {} //析构函数

    void input(int endTag);

    void output();
};

void List ::input(int endTag)
{

    LinkNode *newnode;
    int val;

    cin >> val;

    while (val != endTag)

    {

        newnode = new LinkNode(val);

        if (newnode == NULL)

        {
            cerr << "存储分配错误" << endl;
            exit(1);
        }

        newnode->link = first->link;

        first->link = newnode;

        cin >> val;
    }
}

void List::output()
{
    int flag = 1;
    LinkNode *p = first->link;
    if (p != NULL)
    {
        while (p != NULL)
        {
            if (flag)
            {
                cout << p->data<<endl;
                flag = 0;
            }
            else
            {
                flag = 1;
            }
            p = p->link;
        }
    }
    else
    {
        cout << 1;
    }
}

int main()

{

    List l;

    l.input(0);

    l.output();

    return 0;
}

/* PRESET CODE END - NEVER TOUCH CODE ABOVE */

3.二叉树

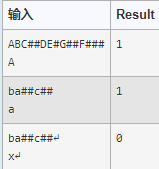
编写函数Find,查询二叉树中是否存在某个字符，如果存在则返回1，否则返回0.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
/* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */

#include <iostream>

using namespace std;

class BinaryTree;

class BinTreeNode
{ //结点类的定义

    friend struct BinaryTree;

public:
    BinTreeNode(char x, BinTreeNode *left = NULL, BinTreeNode *right = NULL) : data(x), leftChild(left), rightChild(right) {} //构造函数

    ~BinTreeNode() {} //析构函数

private:
    BinTreeNode *leftChild, *rightChild; //左、右子女链域

    char data; //数据域
};

class BinaryTree
{

public:
    BinaryTree(char value)
    {
        EndTag = value;
        root = NULL;
    }

    void CreateBinTree() { CreateBinTree(root); }

    int Find(char value) { return Find(root, value); }

private:
    BinTreeNode *root; //二叉树的根指针

    char EndTag; //数据输入停止标志

    void CreateBinTree(BinTreeNode *&subTree);

    int Find(BinTreeNode *subTree, char value);
};

void BinaryTree ::CreateBinTree(BinTreeNode *&subTree)
{ //私有函数: 建立根为subTree的子树

    char item;
    cin >> item;

    if (item != EndTag)
    {

        subTree = new BinTreeNode(item);

        CreateBinTree(subTree->leftChild);

        CreateBinTree(subTree->rightChild);
    }

    else
        subTree = NULL;
};
int flag = 0;
int BinaryTree::Find(BinTreeNode *subTree, char value)
{
    if (subTree != NULL)
    {
        Find(subTree->leftChild, value);
        Find(subTree->rightChild, value);
        if (subTree->data == value)
        {
            flag = 1;
        }
    }
    if (flag)
        return 1;
    else
        return 0;
}

int main()

{

    BinaryTree a = BinaryTree('#');

    a.CreateBinTree();

    char findwhat;

    cin >> findwhat;

    cout << a.Find(findwhat) << endl;
}

/* PRESET CODE END - NEVER TOUCH CODE ABOVE */

4.图

通过编程实现求无向图中某个顶点的度。说明：

1）无向图采用 邻接矩阵存储；

2）主函数已给出，输入参数的说明见main函数的备注;

3）权值的取值范围为(0~maxWeight);

4）对角线上的权值为0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
/* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */

#include "iostream"

#include "stdlib.h"

using namespace std;

typedef int E; //边的权值 的数据类型

typedef char T; //顶点值 的数据类型

#define maxWeight 100

class Graphmtx
{

private:
    T *VerticesList; //顶点表

    E **Edge; //邻接矩阵

    int numVertices;

    int maxVertices;

    int numEdges;

public:
    Graphmtx(int sz = 20); //构造函数

    ~Graphmtx()
    {
        delete[] VerticesList;
        delete[] Edge;
    }

    bool insertVertex(const T vertex); //插入顶点vertex

    bool insertEdge(int v1, int v2, E cost); //插入边(v1, v2),权值为cost

    int getDegree(int VerticeIndex); // 查找下标为VerticeIndex的节点的度
};

Graphmtx::Graphmtx(int sz)
{ //构造函数

    maxVertices = sz;

    numVertices = 0;
    numEdges = 0;

    int i, j;

    VerticesList = new T[maxVertices]; //创建顶点表

    Edge = new E *[maxVertices];

    for (i = 0; i < maxVertices; i++)

        Edge[i] = new E[maxVertices]; //邻接矩阵

    for (i = 0; i < maxVertices; i++) //矩阵初始化

        for (j = 0; j < maxVertices; j++)

            Edge[i][j] = (i == j) ? 0 : maxWeight; //maxWeight
};

bool Graphmtx::insertVertex(const T vertex)
{ //插入顶点 vertex

    if (numVertices == maxVertices)
        return false;

    VerticesList[numVertices++] = vertex;

    return true;
};

bool Graphmtx::insertEdge(int v1, int v2, E cost)
{

    //插入一条起始顶点为v1、终止顶点为 v2的边

    if (v1 < 0  v1 >= numVertices  v2 < 0  v2 >= numVertices)

    {
        cout << "参数v1或v2越界出错!" << endl;
        return false;
    }

    Edge[v1][v2] = cost;
    Edge[v2][v1] = cost; //插入边

    numEdges++; //边的个数加1

    return true;
}

int Graphmtx::getDegree(int VerticeIndex)
{
    int result = 0;
    for (int i = 0; i < numVertices; i++)
    {
        if (Edge[VerticeIndex][i] != 0 && Edge[VerticeIndex][i] != maxWeight)
        {
            result++;
        }
    }
    return result;
}

int main()

{

    Graphmtx a;

    int Vertices;

    cin >> Vertices; //读入顶点的个数

    for (int i = 1; i <= Vertices; i++)

    {
        T value;

        cin >> value;

        a.insertVertex(value);
    } // 读入每个顶点的值

    int Edges;

    cin >> Edges; // 读入边的条数

    for (int i = 1; i <= Edges; i++)
    {

        int row, col, weight;

        cin >> row >> col >> weight; // 读入要插入的边（行号，列号，权值）

        a.insertEdge(row, col, weight);
    }

    int whichVertice;

    cin >> whichVertice; //读入待求节点的下标

    cout << a.getDegree(whichVertice) << endl; //求下标为whichVertice的顶点的度。

    return 0;
}

/* PRESET CODE END - NEVER TOUCH CODE ABOVE */

5.哈希存储

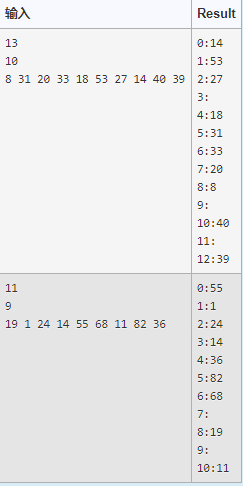
编写程序实现Hash存储，Hash函数是H（key）=key%N (N从键盘输入，在main函数中读入)，其中%是求余运算。用二次探查法解决冲突。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
/* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW */

#include <iostream>

using namespace std;

int Hash(int* s, int N)
{
    int num;
    int key = N;
    cin >> num;
    int* s1 = new int[num];
    for (int i = 0; i < num; i++)
    {
        cin >> s1[i];
    }
    for (int i = 0; i < key; i++)
    {
        s[i] = 0;
    }
    for (int i = 0; i < num; i++)
    {
        int mod = s1[i] % key;
        if (s[mod] == 0)
        {
            s[mod] = s1[i];
        }
        else
        {
            int d0 = mod;
            int d1 = 1;
            while (1)
            {
                mod = (d0 + d1 * d1) % key;
                if (s[mod] == 0)
                {
                    s[mod] = s1[i];
                    break;
                }
                else
                {
                    mod = (d0 + key - d1 * d1) % key;
                    
                    if (s[mod] == 0)
                    {
                        s[mod] = s1[i];
                        break;
                    }
                }
                d1++;
            }
        }
    }
    return 0;
}

int main()

{   int N;

    cin>>N;

int *s= new int[N];



Hash(s,N);

for (int i=0;i<N;i++)

{ 

  cout<<i<<":";

  if (s[i]!=0)  //0表示该存储单元没有存放数据；

 cout <<s[i];  

  cout<<endl;

}

return 0;

}

/* PRESET CODE END - NEVER TOUCH CODE ABOVE */