存储方式

设矩阵 A 中有 s 个非零元素，若 s 远远小于矩阵元素的总数（即s≤m×n），则称 A 为稀疏矩阵。e=s/(m*n),为矩阵的稀疏因子。有人认为 e≤0.05 时称之为稀疏矩阵。

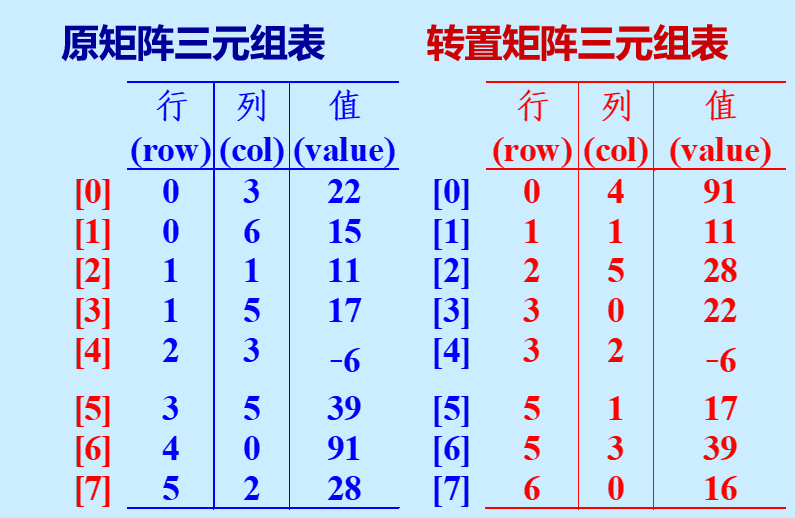
每一个三元组 (i, j, aij) 唯一确定了矩阵A的一个非零元素。因此，稀疏矩阵可由表示非零元的一系列三元组及其行列数唯一确定。

三元组结构体

1
2
3
4
5
6
7
8
9
10
11
12
13
#include <iostream>
using namespace std;
struct Triple
{                             //三元组
    int row, col;             //非零元素行号/列号
    int value;                //非零元素的值
    void operator=(Triple &R) //赋值
    {
        row = R.row;
        col = R.col;
        value = R.value;
    }
};

稀疏矩阵类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class SparseMatrix
{
private:
    int Rows, Cols, Terms; //行／列／非零元素数
    Triple *smArray;       //三元组表
public:
    SparseMatrix(int Rw, int Cl, int Tm); //构造函数
    void Transpose(SparseMatrix &b);      //转置
};
SparseMatrix::SparseMatrix(int Rw, int Cl, int Tm)
{
    Rows = Rw;
    Cols = Cl;
    Terms = Tm;
    smArray = new Triple[Terms]; //三元组表
    if (smArray == NULL)
    {
        cout << “存储分配失败！” << endl;
        exit(1);
    }
};

转置算法

一个 m*n 的矩阵 A，它的转置矩阵 B 是一个 n*m 的矩阵，且A[_i_][_j_] = B[_j_][_i_]。即 矩阵 A 的行成为矩阵 B 的列 矩阵 A 的列成为矩阵 B 的行。

在稀疏矩阵的三元组表中，非零矩阵元素按行存放。当行号相同时，按列号递增的顺序存放。

扫描列的转置算法

算法思想：

  1. 每次从源矩阵中复制一列到新矩阵中
  2. 设矩阵列数为 Cols，对矩阵三元组表扫描Cols 次:
  3. 第 k 次扫描找寻所有列号为 k 的项:将其行号变列号、列号变行号，顺次存于转置矩阵三元组表。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void SparseMatrix::Transpose(SparseMatrix &B)
{
    //转置this矩阵，转置结果由B返回
    B.Rows = Cols;
    B.Cols = Rows;
    B.Terms = Terms;
    //转置矩阵的列数,行数和非零元素个数

    if (Terms == 0)
        return;
    int CurrentB = 0;          //转置三元组表存放下标
    int i, k;
    for (k = 0; k < Cols; k++) //处理所有列号
        for (i = 0; i < Terms; i++)
            if (smArray[i].col == k)
            {
                B.smArray[CurrentB].row = k;
                B.smArray[CurrentB].col = smArray[i].row;
                B.smArray[CurrentB].value = smArray[i].value;
                CurrentB++;
            }
}

算法缺点：

  • 设矩阵三元组表总共有t项，上述算法代价为O（n*t）
  • 若矩阵有200行，200列，1000个非零元素，总共有200000次处理

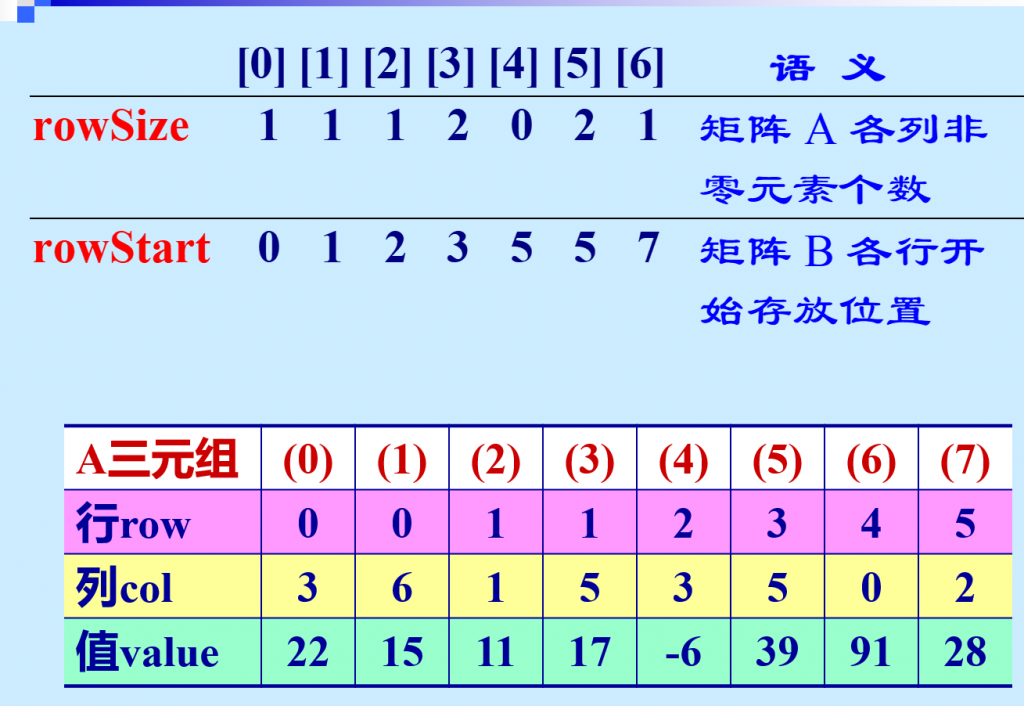
快速转置算法

为加速转置速度，建立辅助数组 rowSize 和 rowStart： rowSize记录矩阵转置前各列，即转置矩阵各行非零元素个数； rowStart记录各行非零元素在转置三元组表中开始存放位置。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void SparseMatrix::FastTranspos(SparseMatrix &B)
{
    int *rowSize = new int[Cols];  //列元素数数组
    int *rowStart = new int[Cols]; //转置位置数组
    B.Rows = Cols;
    B.Cols = Rows;
    B.Terms = Terms;
    if (Terms > 0)
    {
        int i, j;
        for (i = 0; i < Cols; i++)
            rowSize[i] = 0;
        for (i = 0; i < Terms; i++)
            rowSize[smArray[i].col]++;
        rowStart[0] = 0;
        for (i = 1; i < Cols; i++)
            rowStart[i] = rowStart[i - 1] + rowSize[i - 1];
        for (i = 0; i < Terms; i++)
        {
            j = rowStart[smArray[i].col];
            B.smArray[j].row = smArray[i].col;
            B.smArray[j].col = smArray[i].row;
            B.smArray[j].value = smArray[i].value;
            rowStart[smArray[i].col]++;
        }
    }
    delete[] rowSize;
    delete[] rowStart;
}
  • 时间复杂性：O(2Cols+2Terms)
  • 当Terms << Rows*Cols时，比一般转置算法快，所以又称为快速转置算法。
  • 在空间复杂性上，该算法多用了两个辅助向量，是以少量空间换取了较快的执行速度。