实现稀疏矩阵压缩存储,并实现矩阵转置和求和。
输入矩阵时,首先需要输入非零元素的个数,然后分别输入矩阵的 行号,列号和值。
输完2个矩阵后,自动进行计算第一个矩阵的转置以及两个矩阵的和。
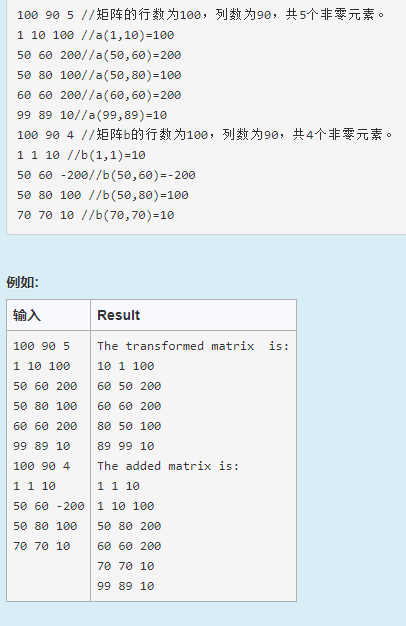
例如:输入如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
| #include <iostream>
using namespace std;
struct Triple
{
int row, col;
int value;
void operator=(Triple &R)
{
row = R.row;
col = R.col;
value = R.value;
}
void output()
{
cout << row << ' ' << col << ' ' << value << endl;
}
};
class SparseMatrix
{
private:
int Rows, Cols, Terms;
public:
Triple *smArray;
SparseMatrix(int Rw, int Cl, int Tm);
void Transpose(SparseMatrix &b);
void Add(SparseMatrix &a);
};
SparseMatrix::SparseMatrix(int Rw, int Cl, int Tm)
{
Rows = Rw;
Cols = Cl;
Terms = Tm;
smArray = new Triple[Terms];
}
void SparseMatrix::Transpose(SparseMatrix &B)
{
int *rowSize = new int[Cols];
int *rowStart = new int[Cols];
B.Rows = Cols;
B.Cols = Rows;
B.Terms = Terms;
if (Terms > 0)
{
int i, j;
for (i = 0; i < Cols; i++)
rowSize[i] = 0;
for (i = 0; i < Terms; i++)
rowSize[smArray[i].col]++;
rowStart[0] = 0;
for (i = 1; i < Cols; i++)
rowStart[i] = rowSize[i - 1] + rowStart[i - 1];
for (i = 0; i < Terms; i++)
{
j = rowStart[smArray[i].col];
B.smArray[j].row = smArray[i].col;
B.smArray[j].col = smArray[i].row;
B.smArray[j].value = smArray[i].value;
rowStart[smArray[i].col]++;
}
cout << "The transformed matrix is:" << endl;
for (int k = 0; k < Terms; k++)
{
B.smArray[k].output();
}
delete[] rowSize;
delete[] rowStart;
}
}
void SparseMatrix::Add(SparseMatrix &b)
{
SparseMatrix result(Rows, Cols, 0);
if (Rows != b.Rows Cols != b.Cols)
{
cout << "无法相加" << endl;
return;
}
int i = 0, j = 0, index1, index2;
while (i < Terms && j < b.Terms)
{
index1 = Cols * smArray[i].row + smArray[i].col;
index2 = Cols * b.smArray[j].row + b.smArray[j].col;
if (index1 > index2)
{
result.smArray[result.Terms] = b.smArray[j];
j++;
}
else if (index1 < index2)
{
result.smArray[result.Terms] = smArray[i];
i++;
}
else
{
smArray[i].value = smArray[i].value + b.smArray[j].value;
if (smArray[i].value != 0)
{
result.smArray[result.Terms] = smArray[i];
}
if (smArray[i].value == 0)
{
result.Terms--;
}
i++;
j++;
}
result.Terms++;
}
while (i < Terms)
{
result.smArray[result.Terms] = smArray[i];
result.Terms++;
i++;
}
while (j < b.Terms)
{
result.smArray[result.Terms] = b.smArray[j];
result.Terms++;
j++;
}
cout << "The added matrix is:" << endl;
for (int k = 0; k < result.Terms; k++)
{
result.smArray[k].output();
}
}
int main()
{
int a1, b1, c1, a2, b2, c2;
cin >> a1 >> b1 >> c1;
SparseMatrix A(a1, b1, c1), B(a1, b1, c1);
Triple Tri1, Tri2;
for (int i = 0; i < c1; i++)
{
cin >> Tri1.row >> Tri1.col >> Tri1.value;
A.smArray[i].operator=(Tri1);
}
cin >> a2 >> b2 >> c2;
SparseMatrix C(a2, b2, c2);
for (int j = 0; j < c2; j++)
{
cin >> Tri2.row >> Tri2.col >> Tri2.value;
C.smArray[j].operator=(Tri2);
}
A.Transpose(B);
A.Add(C);
return 0;
}
|

