特殊矩阵的压缩矩阵

特殊矩阵是指非零元素或零元素的分布有一定规律的矩阵。特殊矩阵的压缩存储主要是为节省存储空间，对可以不存储的元素，如零元素或对称元素，不再存储。

特殊矩阵的分类：

下三角矩阵

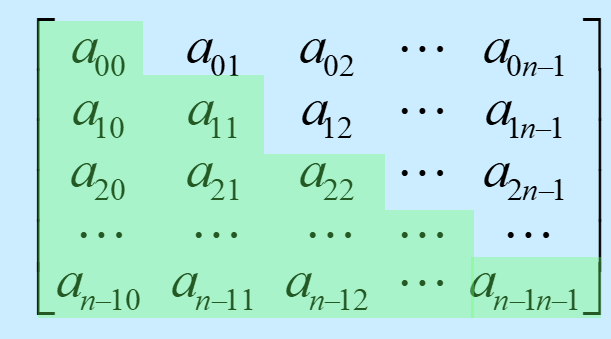
把它们按行存放于一个一维数组 B 中，称之为对称矩阵 A 的压缩存储方式。

数组B共有n + ( n - 1 ) +…… + 1 =n*(n+1)／2 个元素

若i>=j，数组元素A[i][j]在数组B中的存放位置为1 + 2 +……+ i + j = (i + 1)* i / 2 + j

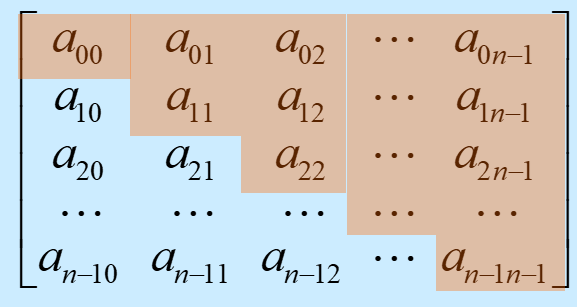
数组B共有n + ( n - 1 ) +…… + 1 =n*(n+1)／2 个元素

若i <=j，数组元素A[i][j]在数组B中的存放位置为 n + (n-1) + (n-2) +……+ (n-i+1) + j-i

特点：

三对角矩阵中除主对角线及在主对角线上下最临近的两条对角线上的元素外，所有其它元素均为0。总共有3n-2（n>2）个非零元素。
将三对角矩阵A中三条对角线上的元素按行存放在一维数组 B 中，且_a_00存放于B[0]。
xxxxxxxxxx /* PRESET CODE BEGIN - NEVER TOUCH CODE BELOW /#include using namespace std;int Hash(int s, int N){ int num; int key = N; cin >> num; int* s1 = new int[num]; for (int i = 0; i < num; i++) { cin >> s1[i]; } for (int i = 0; i < key; i++) { s[i] = 0; } for (int i = 0; i < num; i++) { int mod = s1[i] % key; if (s[mod] == 0) { s[mod] = s1[i]; } else { int d0 = mod; int d1 = 1; while (1) { mod = (d0 + d1 * d1) % key; if (s[mod] == 0) { s[mod] = s1[i]; break; } else { mod = (d0 + key - d1 * d1) % key; if (s[mod] == 0) { s[mod] = s1[i]; break; } } d1++; } } } return 0;}int main(){ int N; cin>>N;int s= new int[N];Hash(s,N);for (int i=0;i<N;i++){ cout<<i<<”:”; if (s[i]!=0) //0表示该存储单元没有存放数据； cout <<s[i]; cout<<endl;}return 0;}/ PRESET CODE END - NEVER TOUCH CODE ABOVE */c++

压缩方法：

在一维数组 B 中A[i][j]在第 i 行，它前面有3*i-1个非零元素，在本行中第 j 列前面有j-i+1个，所以元素A[i][j]在B 中位置为k=2*i+j