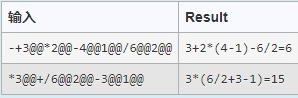
将通过二叉链表实现的表达式二叉树进行输出,同时计算出结果。
要求:
1)二叉树建立时,使用先序建立;
2)四个运算符包括:+, -, *, /;
3 ) 在输出时,遇到优先级问题时,相应的括号也要输出。
提示:
1)递归执行下列步骤即可求值:先分别求出左子树和右子树表示的子表达式的值,最后根据根结点的运算符的要求,计算出表达式的最后结果。
2)二叉树的中序遍历序列与原算术表达式基本相同,但是需要将中序序列加上括号,即当根结点运算符优先级高于左子树(或右子树)根结点运算符时,就需要加括号。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
| #include "cstdio"
#include <cmath>
#include <iostream>
#include <stdio.h>
using namespace std;
class Tree;
class TreeNode
{
friend class Tree;
private:
char data;
TreeNode *left;
TreeNode *right;
public:
TreeNode() : left(NULL), right(NULL){};
TreeNode(char data1) : data(data1), left(NULL), right(NULL) {}
};
class Tree
{
private:
TreeNode *root;
char endtag;
void createTree(TreeNode *&subtree);
void destroy(TreeNode *&subtree);
void inorder(TreeNode *subtree);
int operator1(TreeNode *subtree);
public:
Tree() { root = NULL; }
Tree(char end1, TreeNode *p = NULL) : root(p), endtag(end1) {}
bool isEmpty() { return root == NULL ? true : false; }
void createTree() { createTree(root); }
void inorder() { inorder(root); }
int operator1() { return operator1(root); }
bool see(char op1, char op2);
};
void Tree::createTree(TreeNode *&subtree)
{
char item;
cin >> item;
if (item != endtag)
{
subtree = new TreeNode(item);
createTree(subtree->left);
createTree(subtree->right);
}
}
void Tree::destroy(TreeNode *&subtree)
{
if (subtree != NULL)
{
destroy(subtree->left);
destroy(subtree->right);
delete subtree;
}
}
void Tree::inorder(TreeNode *subtree)
{
if (subtree != NULL)
{
if (subtree->right != NULL && see(subtree->data, subtree->right->data))
{
inorder(subtree->left);
cout << subtree->data;
cout << '(';
inorder(subtree->right);
cout << ')';
}
else
{
inorder(subtree->left);
cout << subtree->data;
inorder(subtree->right);
}
}
}
int Tree::operator1(TreeNode *subtree)
{
if (subtree != NULL)
{
switch (subtree->data)
{
case '+':
return operator1(subtree->left) + operator1(subtree->right);
break;
case '-':
return operator1(subtree->left) - operator1(subtree->right);
break;
case '*':
return operator1(subtree->left) * operator1(subtree->right);
break;
case '/':
return operator1(subtree->left) / operator1(subtree->right);
break;
default:
return int(subtree->data - '0');
break;
}
}
else
return 0;
}
bool Tree::see(char op1, char op2)
{
if ((op1 == '*' op1 == '/') && (op2 == '+' op2 == '-'))
return true;
else
return false;
}
int main()
{
Tree tree('@');
tree.createTree();
tree.inorder();
cout << '=' << tree.operator1() << endl;
return 0;
}
|
