原理：

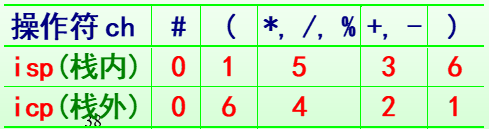
使用两个栈操作符栈OPTR (operator)，操作数栈OPND(operand)，为了实现这种计算，需要考虑各操作符的优先级

代码思路：

  1. 建立并初始化OPTR栈和OPND栈，然后在OPTR栈中压入一个“#”
  2. 扫描中缀表达式，取一字符送入ch。
  3. 当ch != ‘#’ 或OPTR栈的栈顶 != ‘#’时, 执行以下工作, 否则结束算法。在OPND栈的栈顶得到运算结果。

循环过程：

  1. 若ch是操作数，进OPND栈，读下一字符到ch；
  2. 若ch是操作符，比较icp(ch)的优先级和isp(OPTR)的优先级：
    • 若icp(ch) > isp(OPTR)，则ch进OPTR栈，读下一字符到ch；
    • 若icp(ch) < isp(OPTR)，则从OPND栈退出a2和a1，从OPTR栈退出θ, 形成运算指令 (a1)θ(a2)，结果进OPND栈,不读入下一字符而是继续比较栈顶元素；
    • 若icp(ch) == isp(OPTR) 且ch == ‘)’，则从OPTR栈退出’(‘，对消括号，然后从中缀表达式取下一字符送入ch；

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
#include <iostream>

using namespace std;
class LinkedStack;
class LinkedStack2;
class StackNode
{
    friend class LinkedStack;

public:
    StackNode *link;
    char data;
    float data2;

public:
    StackNode(StackNode *ptr = NULL)
    {
        link = ptr;
    }
    StackNode(char &c, StackNode *ptr = NULL)
    {
        data = c;
        link = ptr;
    }
    StackNode(float &c, StackNode *ptr = NULL)
    {
        data2 = c;
        link = ptr;
    }
};
class LinkedStack
{ //链式栈类定义
public:
    StackNode *top; //栈顶指针
public:
    LinkedStack(); //构造函数
    char getTop(char &ch);
    void Push(char &ch); //进栈
    int Pop(char &ch);   //退栈
    float getTop(float &ch);
    void Push(float &ch); //进栈
    int Pop(float &ch);   //退栈
    void makeEmpty();    //清空栈的内容
    int IsEmpty() { return (top == NULL) ? 1 : 0; }
};
LinkedStack::LinkedStack()
{
    top = NULL;
}
char LinkedStack::getTop(char &ch)
{
    ch = top->data;
    return ch;
}
float LinkedStack::getTop(float &ch)
{
    ch = top->data2;
    return ch;
}
void LinkedStack::makeEmpty()
{
    if (top != NULL)
    {
        StackNode *p = top->link;
        while (top != NULL)
        { //逐个结点释放
            p = top;
            top = top->link;
            delete p;
        }
    }
}
void LinkedStack::Push(char &ch)
{
    top = new StackNode(ch, top); //创建新结点
}
void LinkedStack::Push(float &ch)
{
    top = new StackNode(ch, top); //创建新结点
}
int LinkedStack::Pop(char &ch)
{
    //删除栈顶结点, 返回被删栈顶元素的值。
    if (IsEmpty())
        return 0;       //栈空返回
    StackNode *p = top; //暂存栈顶元素
    top = top->link;    //退栈顶指针
    ch = p->data;
    delete p; //释放结点
    return 1;
}
int LinkedStack::Pop(float &ch)
{
    //删除栈顶结点, 返回被删栈顶元素的值。
    if (IsEmpty())
        return 0;       //栈空返回
    StackNode *p = top; //暂存栈顶元素
    top = top->link;    //退栈顶指针
    ch = p->data2;
    delete p; //释放结点
    return 1;
}

int isp(char &c)
{
    //返回栈内优先级
    if (c == '#')
    {
        return 0;
    }
    else if (c == '(')
    {
        return 1;
    }
    else if (c == ')')
    {
        return 6;
    }
    else if (c == '+'  c == '-')
    {
        return 3;
    }
    else
    {
        return 5;
    }
}
int icp(char &c)
{
    //返回栈外优先级
    if (c == '#')
    {
        return 0;
    }
    else if (c == '(')
    {
        return 6;
    }
    else if (c == ')')
    {
        return 1;
    }
    else if (c == '+'  c == '-')
    {
        return 2;
    }
    else
    {
        return 4;
    }
}
void Calculator() //把中缀表达式e转换成后缀表示并输出
{
    LinkedStack OPTR,OPND;
    float ch2;
    char ch = '#', ch1, op;
    OPTR.Push(ch);
    cin.get(ch);
    while (ch != '#'  OPTR.getTop(ch1) != '#')
    {
        if (isdigit(ch))
        {
            cin.putback(ch); //回退一下，
            cin >> ch2;      //读取操作数
            cin.get(ch);
            OPND.Push(ch2);
        }
        else
        {
            OPTR.getTop(ch1);
            if (icp(ch) > isp(ch1))
            {

                OPTR.Push(ch);
                cin.get(ch);
            }
            else if (icp(ch) < isp(ch1))
            {
                float right, left, value;
                OPTR.Pop(op);
                OPND.Pop(right);
                OPND.Pop(left);
                if (op == '+')
                {
                    value = left + right;
                    OPND.Push(value);
                }
                else if (op == '-')
                {
                    value = left - right;
                    OPND.Push(value);
                }
                else if (op == '*')
                {
                    value = left * right;
                    OPND.Push(value);
                }
                else
                {
                    if (right == 0.0)
                    {
                        cerr << "Divide by 0 !" << endl;
                        ch = '#';
                        OPTR.Push(ch);
                    }
                    else
                    {
                        value = left / right;
                        OPND.Push(value);
                    }
                }
            }
            else
            {
                if (ch == ')')
                {
                    OPTR.Pop(op);
                    cin.get(ch);
                }
            }
        }
    }
    float result;
    OPND.getTop(result);
    cout << result;
}
int main()
{
    Calculator();
    return 0;
}